고정 헤더 영역
상세 컨텐츠
본문
1. Decision Tree Classifiers
- 우리가 알고싶은 함수를 트리로 표현하고 학습하는 방법
- 예시) PlayTennis : "오늘 테니스를 칠까?"라는 질문에 대해 주어진 정보를 바탕으로 Yes/No 예측
- 트리의 구성 요소 :
1) internal node : 어떤 속성 Xi를 테스트함 ex. Outlook
2) branch : 속성 Xi의 값 하나에 해당하는 분기 ex. Outlook=Sunny
3) leaf node : 최종적인 예측 결과 Y ex. PlayTennis=No


2. Decision Tree 학습 문제 정의
1) 입력 : 특성 벡터와 정답 레이블의 쌍 { x^(i), y^(i) } *여기서의 입력은 머신러닝 알고리즘(모델)의 입력값으로, 학습을 하는 과정을 통해 결정 트리를 만들어냄(출력)
2) 목표 함수 : 우리가 모르는 함수( f : X→Y )로, 학습을 통해 추정해야 함
ex. → 테니스 침
3) 출력 : 목표함수 f를 가장 잘 근사하는 가설함수 h∈H
- H는 가능한 가설 함수들의 집합
- 가설 h는 결정트리로 표현됨
3. Decision Tree 핵심 개념
- 핵심 질문 1: 어떻게 훈련 데이터를 잘 설명하는 가설을 찾을까?
- 핵심 질문 2: 그 가설이 새로운 데이터(테스트 데이터)에서도 잘 작동할까? 즉, generalization이 잘 되는지가 중요
- 데이터와 일치하는 가설들 중 가장 단순한 것을 선택
- 데이터를 잘 설명하는 작은 decision tree를 찾는다면, 일반화 보장 → 이를 위해 ID3 같은 Top-down 알고리즘을 사용
4. ID3: Top-Down Induction of Decision Trees
- 루트부터 시작해서 리프까지 재귀적으로 분할해 나가는 방식
- Greedy 방식을 사용해 전체를 다 탐색하지 않고 매 순간 최적인 선택만 함(휴리스틱 탐색)
- 학습 데이터가 완전히 분류되면, 더 이상 트리를 키우지 않음(가장 작은 트리)
- 간단한 트리를 선호 → 과적합 가능성
- 가지치기(pruning)가 도움이 될 수 있음
- 알고리즘 :
1) 루트를 분할할 최선의 속성 선택
2) 자식 노드가 impure할 경우 계속 분기
- 가장 좋은 속성을 어떻게 고를까? → Information Gain이 가장 높은 속성을 고름
5. Information Gain
- 주어진 속성이 훈련 예제를 얼마나 잘 구분하는지를 나타내는 통계적 척도
- 특정 속성 A로 데이터를 나눴을 때, 그 데이터의 엔트로피가 얼마나 줄어드는지 측정하는 방법

- Entropy : 데이터셋 S의 불확실성(impurity)을 측정하는 지표로, 클래스가 얼마나 섞여있는지를 수치화
- p+ : positive 클래스의 비율, p− : negative 클래스의 비율
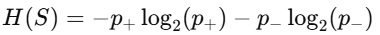
- 모두 positive하거나 모두 negative하면 엔트로피는 0
- 반은 positive, 반은 negative하면 엔트로피는 1(가장 불확실)
- 이진 분류의 경우 엔트로피의 범위는 [0, 1]
- 만약 클래스가 둘이 아니라 셋 이상이면?(Boolean이 아닌 경우)

- c개의 클래스가 있을 경우 엔트로피의 범위는 [0, log2c]
- 데이터를 어떤 속성 A로 나누었을 때, 엔트로피가 많이 줄어들면 좋은 속성임
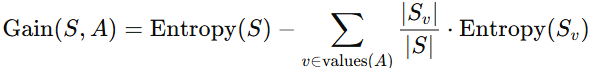
6. Overfitting in Decision Trees
- 데이터에 노이즈가 있을 때 발생
- 트리가 학습 데이터에만 맞게 학습되어 새로운 데이터에 대한 예측이 나빠지는 현상
- : 트리 h가 학습 데이터에서 틀린 비율
- : 트리 가 전체 진짜 데이터(미래 포함)에서 틀릴 확률
- 가 과적합(overfit)한 경우란?
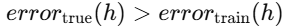

- 과적합 막는 방법 :
1) 데이터 분할이 유의미하지 않을 때 트리 멈추기
2) 트리를 끝까지 만든 후 불필요한 분기 잘라내기
'머신러닝' 카테고리의 다른 글
| Regression(2) (0) | 2025.04.18 |
|---|---|
| Regression (0) | 2025.04.18 |
| Classification(2) (0) | 2025.04.15 |
| Classification(1) (0) | 2025.04.15 |
| 확률이론(2) (2) | 2025.04.13 |




