고정 헤더 영역
상세 컨텐츠
본문
1. Notations
- Zm = {0,1,...,m−1} : m으로 나눈 나머지의 집합
- g mod p: g를 로 나눈 나머지
- Plaintext space = Ciphertext space = Z26 (알파벳 개수 26개)
- 각 문자의 숫자값을 고정된 키 K만큼 이동시키는 암호 방식
- Enc(K,x) = (x+K) mod26
- Dec(K,Y) = (Y−K) mod26
- 가능한 공격 방법 :
1) Brute-force Attack : 가능한 키는 0 ~ 25 → 총 26가지밖에 없음
2) Known Plaintext Attack : 원문과 암호문을 쌍으로 알고 있을 때 키를 쉽게 계산할 수 있음
3. Affine Cipher
- 는 키 쌍, α,β ∈ Z26
- 는 26과 서로소이어야 함 → gcd(α, 26) = 1
- Enc(K,x) = (αx+β) mod26
- Dec(K,Y) = α^(−1)(Y−β) mod26
- 예를들어 K = (7,3)이고 Y는 0일 때, 7^(-1)*(0-3) mod26을 구해야 하면
1) 1/7은 모듈러 연산을 할 수 없으므로 7*x = 1 mod26이 되는 x를 찾기
2) x = 15이면, 1/7 대신에 15를 넣기
3) 결국 15*(-3) mod26을 구하면 됨.
- 가능한 공격 방법 :
1) Brute-force Attack : 가능한 (α,β)쌍은 총 12*26 = 312 (26과의 서로소는 12개만 가능하므로)
2) Known Plaintext Attack : 원문-암호문 쌍 두 개만 있으면 (α,β)를 선형 방정식으로 풀 수 있음
4. Substitution Cipher
- 알파벳 26개에 대해 순열을 적용하여 각 문자를 치환하는 방식
- Enc(K,x) = π(x)
- Dec(K,Y) = π^(−1)Y
- 가능한 공격 방법 :
1) Brute-force : 가능한 키 수는 26! → 매우 큼
2) Chosen-plaintext : 문-암호문 쌍이 개 주어지면 나머지 알파벳에 대한 경우의 수는 (26−n)!개로 줄어듦
5. Vigenère Cipher
- 다중 치환 방식을 도입한 고전 암호의 대표적인 예
- K = (k1,k2,…,km)∈(Z26)^m
- Enc(K,x1,…,xm) = (x1+k1,…,xm+km) mod26
- Dec(K,Y1,…,Ym) = (Y1−k1,…,Ym−km) mod26
- 가능한 공격 방법 :
1) Brute-force : 가능한 키의 수는 26^m → 상당히 안전
2) Ciphertext-only Attack : 통계적 분석 기법으로 키 길이를 먼저 추정
3) Known-plaintext Attack : 키 길이 mm만 안다면 매우 쉽게 키를 역추적 가능
6. Permutation Cipher
- 평문의 문자 위치를 키로 주어진 순열에 따라 재배열하는 방식
- : {1,2,...,m}의 순열
-
- 암호화 : (x1,...,xm)⋅P = (Y1,...,Ym)로 표현 가능
- 복호화 : (Y1,...,Ym)⋅P−1=(x1,...,xm)로 표현 가
- 가능한 공격 방법 :
1) Brute-force : 가능한 순열의 개수는 m!
2) Known/Chosen Plaintext : 서로 다른 평문을 m개 주면 대응되는 암호문 분석 → P^{-1} 복원 가능
7. LFSR Cipher
1) LFSR : 0과 1로 구성된 키 스트림(비트)을 생성하는 장치
- 다음 상태의 비트를 이전 상태 비트들의 선형 결합으로 만듬
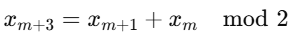
- LFSR의 f(k) 식으로, 이 식을 통해 키 스트림을 만들어냄
- mod2를 하는 이유는 비트로 만들기 위해서(나머지가 0혹은 1로만 나옴)
2) LFSR Cipher : LFSR로 생성된 비트 시퀀스를 키 스트림으로 사용해서 평문 비트와 XOR하는 방식
- Enc(K,(x1, . . . , xm)) = (x1 ⊕ k1, . . . , xm ⊕ km)
- Dec(K,(y1, . . . , ym)) = (y1 ⊕ k1, . . . , ym ⊕ km)
- 가능한 공격 방법 : Known Plaintext Attack
1) 공격자가 평문 (x1,...,xm)과 암호문 (y1,...,ym) 일부를 알고 있다면
키스트림 중 일부를 알 수 있음 yi=xi⊕ki ⇒ ki=xi⊕yi
2) 알아낸 키 스트림을 가지고 행렬 식을 만들면 을 알 수 있음(k가 invertible할 때만)
3) 즉, LFSR의 구조를 알아냈으므로 전체 키 스트림 복원 가능
8. One-Time Pad
- 하나의 키는 반드시 딱 한 번만 사용해야 함
- 장점 : 완벽한 보안
- 평문 길이만큼의 키 필요 : 긴 키를 안전하게 공유하고 저장하기 어려움
'정보보호이론' 카테고리의 다른 글
| Diffie-Hellman Key Exchange (0) | 2025.06.11 |
|---|---|
| Discrete Logarithm Problem (0) | 2025.06.11 |
| Symmetric Encryption(2) (0) | 2025.04.21 |
| Symmetric Encryption(1) (0) | 2025.04.21 |
| Introduction to Information Security and Cryptography (0) | 2025.04.17 |




