고정 헤더 영역
상세 컨텐츠
본문
1. Symmetric Encryption
- 암호화와 복호화에 서로 같은 키를 사용(private key)
- Block Cipher : 입력 데이터를 고정된 크기로 쪼개서 각 블록을 암호화
- Stream Cipher : 데이터를 1비트 단위로 실시간 처리하며 키 스트림과 XOR하여 암호화
2. Block Cipher
- 입력 데이터를 고정된 크기로 쪼개서 각 블록을 암호화
- key 재사용
- 여러 개의 라운드로 이루어진 구조
- 각 라운드에서는 Substitution과 Permutation이 반복됨
3. DES(Data Encryption Standard)
- 블록 암호 설계의 대표적인 구조로 Feistel 구조를 기반으로 만듬
- Feistel 구조의 핵심 원리 :
1) 입력 블록(Plaintext)을 두 부분 L0,R0으로 나눔 → 2w비트 입력 → w비트씩 두 개
2) n번의 라운드를 반복
3) 각 라운드는 다음과같이 이루어짐
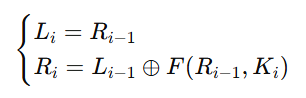
4) 최종적으로 , Rn를 결합하여 암호문을 얻음
- Des의 기본정보 : 평문 블록은 64bits, key는 56bits의 길이, 16라운드(16개의 서브키)
- Initial Permutation : 64비트 평문을 처음에 한번 섞어주는 작업
- Expansion Permutation : 라운드 함수 F의 시작 부분으로, 32비트 Ri-1을 key와 XOR할 수 있도록 48비트로 확장
- S-Boxes : 총 8개가 있고 각 박스에 6비트씩 입력됨. ex. 101110
1) 바깥 2비트가 행 결정 : 10 → row = 2
2) 가운데 4비트가 열 결정 : 0111 → col = 7
3) 그 위치의 값이 출력 4비트로 변환됨
4) 8개의 S-box를 각각 적용하면 4*8 = 32비트로 축소
- Permutation Function : S-box 변환 후 32비트를 단순 재배열함
- Key Schedule : 서브키 생성 과정
1) 64비트 중 56비트로 순열 압축 (C0은 왼쪽 28비트 D0은 오른쪽 28비트)
2) 각 라운드마다 C와 D를 왼쪽으로 회전
3) PC-2 테이블로 48비트 선택해서 서브키 생성

- DES는 전체적으로 선형구조지만 S-box만 비선형 요소
- 즉 S-box가 보안의 핵심 역할
- 전체 가능한 key의 수는 2^56 -> brute force attack 가능
4. Triple DES
- 기존 DES의 단점을 보완하기 위해 고안된 방식
- 평문을 3번 연속으로 DES 알고리즘에 통과
- 총 56*3 = 168개의 key
- 암호화 순서는 Encrypt → Decrypt → Encrypt
- 복호화는 Decrypt → Encrypt → Decrypt
5. AES(Advanced Encryption Standard)
- AES는 DES와 Triple DES를 대체하기 위해 개발
- Hexadecimal Notation (16진수 표현) 사용
- 모든 블록 사이즈는 128비트, key 사이즈는 128, 192, 256비트가 있음
- 라운드 수는 10, 12, 14라운드 존재
- 입력 128비트는 4*4바이트 행렬로 변환
- 한 라운드는 4가지 연산으로 구성돼 있음
1) Substitution bytes: 각 바이트를 S-box를 통해 치환
- 입력 x는 8비트로 GF(2^8)에서 역원을 구함
- 역원을 구한 후 행렬을 사용해 새로운 8비트를 계산
2) Shift Rows: 각 행을 왼쪽으로 이동
3) Mix Columns: 각 열을 이미 정의된 M행렬과 곱하여 새로운 바이트로 바꿈. 1~9라운드에서만 수행
4) Add Round Key: 현재 상태와 해당 라운드 키를 XOR연산으로 결합
- Key Expansion:
1) i가 4의 배수라면 W(i-1)을 왼쪽으로 한 바이트씩 이동(4이 배수가 아니라면 이동x)
2) S-box에 적용
3) r(i) = X^(i-4)/4 를 계산 후 XOR 연산
- 오직 Add Round Key Transformation 단계만 키를 사용
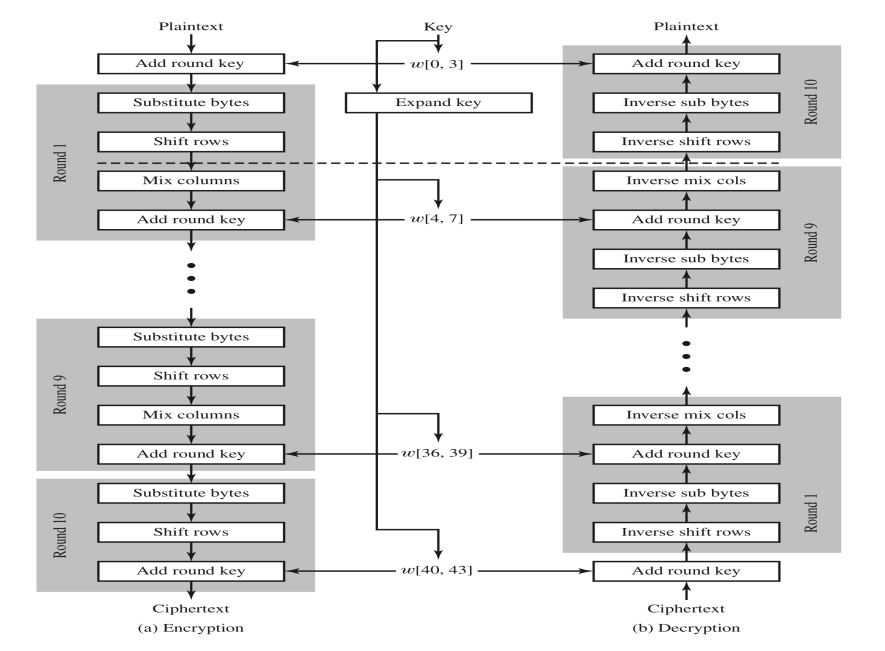
6. Finite Field
- AES에서 자주 등장하는 수학적 배경
- 필드란 덧셈, 뺄셈, 곱셈, 나눗셈 연산을 할 수 있는 수의 집합
- 결합, 분배, 교환법칙 다 성립
- 실수, 유리수, 복소수 등은 필드지만 정수는 필드가 아님
- Finite Field는 소수 p에 대한 정수 집합
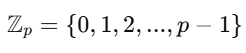
- GF(p^n)은 p^n개의 원소를 갖는 필드
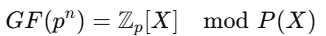
- AES는 GF(2^8)위에서 동작
- AES의 S-box, MixColumns 등은 모두 GF(2⁸) 위에서 연산이 이루어짐
- Z2[x] 는 계수가 0또는 1인 다항식
- P(x) = x8+x4+x3+x+1
7. Extended Euclidean Algorithm
- 두 수의 최대공약수가 1일 때 정수 해(x, y)를 구하는걸 확장 유클리드 알고리즘이라고 함
- 우리가 원하는건 A(x)^(-1) mod P(x)
- A(X)⋅s(X) + P(X)⋅t(X) = gcd(A(x), P(x)) = 1 의 관계를 이용
- gcd는 1이면 역원이 존재하므로, 역추적해 계산
'정보보호이론' 카테고리의 다른 글
| Diffie-Hellman Key Exchange (0) | 2025.06.11 |
|---|---|
| Discrete Logarithm Problem (0) | 2025.06.11 |
| Symmetric Encryption(2) (0) | 2025.04.21 |
| Classical Encryption (0) | 2025.04.17 |
| Introduction to Information Security and Cryptography (0) | 2025.04.17 |




